Etoile |
- cours sur le couplage triphasé
|
|
.

|
- couplage Y -
|
La
plus part des couplages déséquilibrés (équilibré= même courant et même angle de
déphasage) se font en étoile.
Si le couplage est équilibré, il n' a pas besoin de conducteur neutre.
|
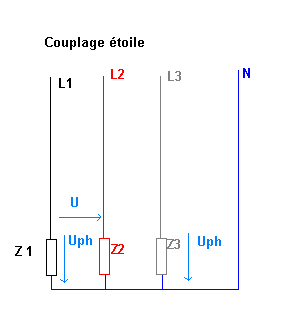
|
La tension U est la différence de potentiel entre deux tensions
de phase donc U vaut la différence vectorielle (géométrique) entre deux
tension de phase. Ce qui nous donne
U = Uph
. 30,5
La tension de phase est décalée de 30 degrés en retard par rapport aux
tension composée.
Le courant de ligne est égale au courant de phase (traversant l'impédance) donc:
I =Iph
sur le réseau : U = 400 [V] et Uph
= 230 [V ]
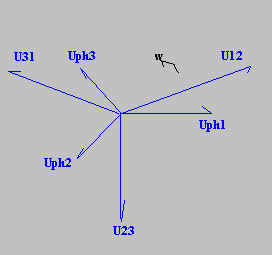
Ci-dessous une representation vectorielle des
tensions de ligne (tensions composées) / tensions de phase et des courants de ligne, de
phase pour un circuit étoile déséquilibré.
- en bleu : clair U ou foncé Uph
- en beige la contruction vetorielle (-Uph) pour trouver U
- en rouge I ou Iph
- en vert la construction vectorielle (+Iph)
pour trouver -Ineutre
- en violet le courant Iph
|
|
Methode de
calcul du courant dans le neutre |
| 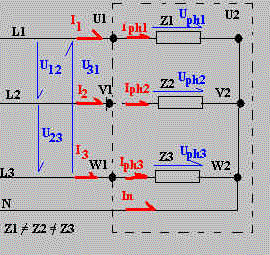 Dans un réseau étoile déséquilibré, une
difficulté est de calculer le courant dans le neutre. Dans un réseau étoile déséquilibré, une
difficulté est de calculer le courant dans le neutre.
Pour cela il existe plusieurs méthodes (attention, les formules parachutées ou la
méthode du triangle ne "marche" que dans certains cas : je vous les
déconseille).
| méthode
graphique: |
par décomposition des
vecteurs |
Dans cette méthode, faut placer tous les courants de
phase par rapport à leur tension de phase en respectant l'angle de déphasage Sur
l'exemple ci-dessous Z1 est purement résistif, Z2 purement
capacitif et Z3 purement inductif.
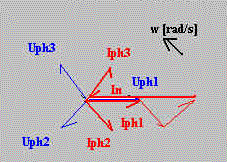
Ensuite, il faut mettre bout à bout chaque courant (l'ordre n'est pas
important) en respectant, l'amplitude, la direction, et le sens de chacun ce qui est une
somme géometrique. La résultante de cette addition corespond au courant dans le neutre
(décalé de 180 degrés). |
Dans cette métode on place le diagramme précédent dans
un système d'axe X-Y (il n'est pas obligatoire de faire coïncider un vecteur avec
un des axes).
Définir l' angle (noté ici a) de
chaque courant par rapport à l'axe X
décomposer les vecteurs en projections X et Y
additionner les projections selon X et selon Y (=résultante)
changer les signes (= projection du neutre)
recalcuer le module (amplitude / intensité) et l'argument (angle
par rapport à X) du courant dans le neutre:
exemple: (un angle f > 0 = inductif)
on suppose Uph1 superposé à l'axe X.
|
|
|
Les puissances en triphasé |
Dans les coupages triphasés, la puissance active totale est égale à la somme des puissances de chaque impédance .
P = P1+P2+
P3
Dans les couplages équilibrés (Z1 = Z2 = Z3,
cos f1 = cos f2
= cos f 3), les calculs se simplifient:
P =3 . P1
|
= 3 . Ur . Ir
|
= 30,5 . U . I
. cos f |
= S . cos f |
Q = 3 . Q1 |
= 3 . Ux . Ix
|
= 30,5 . U .
I . cos f |
=S sin f |
S = 3 . S1 |
= 3 . Uph . Iph |
= 30,5 . U . I
. cos f |
Pythagore ou trigonométrie |
la puissance active = la
somme arithmétique des puissances actives : P = P1+P2+
P3 [W]
la puissance réactive = la
somme algébrique des puissances réactives : Q = Q1+ Q2
+ Q3 [var] (on admettra conventionnelement que si la puissance
réactive est inductive son signe est positif et si elle est capacitif
son signe est négatif)
la puissance apparente = la
somme géométrique des puissances apparentes : addition vectorielle. [VA]
note: Pour des impédances
équivalentes, le couplage triangle est trois fois plus puissant.
panne en étoile avec neutre:
Si un fusible fond dans un couplage étoile avec neutre, sa puissance
n'est plus que des 2/3.
Si une impédance est rompue la puissance n'est plus que des 2/3.
panne en étoile sans neutre:
Si un fusible fond dans un couplage étoile sans neutre, sa puissance
divisée par 2.
Si une impédance est rompue la puissance n'est plus que des 2/3.
|
|
résolution d'exercices : étoile équilibré |
mode d'emploi :
modifiez une valeur (seulement les cases jaunes) et les autres valeurs se
mettent automatiquement à jour. Sur la première ligne si vous modifiez une valeur , par
exemple Z, la tension reste inchangée et c'est la puissance qui est modifiée. Dans la
seconde ligne, c'est la puissance qui est ne change pas et la tension qui s'adapte.
|
|
Résolution d'exercices : étoile deséquilibré |
étoile deséquilibré: (U=400 V, un angle f > 0 = inductif )
mode d'emploi :
modifiez une valeur (seulement les cases jaunes) et les autres valeurs se
mettent automatiquement à jour. Sur la première ligne si vous modifiez une valeur , par
exemple Z, la tension reste inchangée et c'est la puissance qui est modifiée. Dans la
seconde ligne, c'est la puissance qui est ne change pas et la tension qui s'adapte:
Mon conseil , testez :
- Z1 =23, f1 = 0, Z2
=23, f2 = -90, Z3 =23,
f3 = 90
- Z1 =23, f1 = 0, Z2 =23,
f2 = 90, Z3 =23, f3 = - 90
- Z1 =23, f1 = 60, Z2 =23,
f2 = -60, Z3 =infini, f3 = 0
(donnez I3 = 0)
et annalysez la valeur de In....
|
|
|