|
|
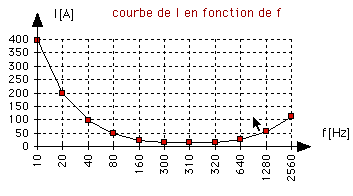 |
Comme on le voit sur la courbe ci-contre, le courant
est maximum pour une fréquence basse ou élevée. Par
contre, il devient minimum à une fréquence intermédiaire. On obtient une telle courbe
lorsqu'on place en parallèle un condensateur,
une self et une résistance (voir l'impédance
RLC)
La fréquence à laquelle le courant est minimum s'appelle fréquence de résonance
et elle se note f0.
à f0 le courant vaut U / R
car Z =R
|
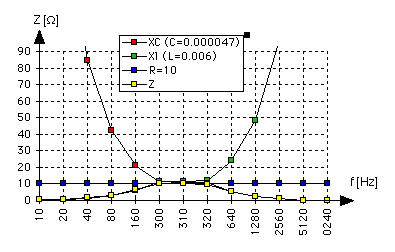
| Sur le graphique, sont représentés Z, R, Xl,
et Xc. On constate que la valeur de l'impédance est au minimum pour une fréquence
basse ou élevée. Par contre, elle devient maximale à la fréquence de résonance.
On remarque que les valeurs des réactances sont identiques à f0,
donc elles s'annulent à cette fréquence.
Ce qui nous permet de donner les définitions suivantes:
|
 |
| à f0 :
- Xl = Xc
- Z = R
- P = S
- le déphasage courant-tension est nul
- Q = 0 [var]
- Ql = Qc
|
ici, je détermine la fréquence de résonance :
|
|
|
|
|
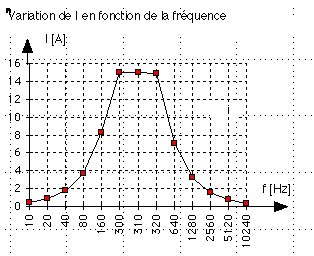 |
Comme on le voit sur la courbe ci-contre, le courant est minimum
pour une fréquence basse ou élevée.
Par contre, il devient maximum à une fréquence intermédiaire. On obtient une telle
courbe lorsqu'on place en série un condensateur,
une self et une résistance (voir
l'impédance RLC)
La fréquence à laquelle le courant est maximum se nomme: fréquence de résonance
et elle se note f0.
à f0 le courant vaut U /
R |
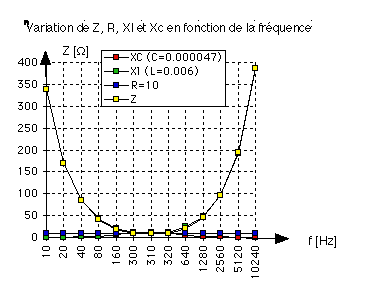
| Sur le graphique, sont représentés Z, R, Xl,
et Xc. On constate que la valeur de l'impédance Z est infinie pour une fréquence
nulle (le condensateur bloque le courant) ou une fréquence infinie (la self bloque le
courant).
Par contre, elle devient minimum à la fréquence de résonance. On
remarque que les valeurs des réactances sont identiques à f0, donc
elles s'annulent à cette fréquence.
Ce qui nous permet de donner la définition suivante:
|
 |
| à f0 :
- Xl = Xc
- Z = R
- P = S
- le déphasage courant-tension est nul
- Q = 0 [var]
- Ql = Qc
|
ici. je détermine la fréquence de résonance :
|
|
|
|
|
Un filtre passe-bas atténues les courants de fréquences élevées ("laisse
passer les basses fréquences").
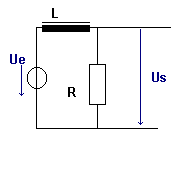 |
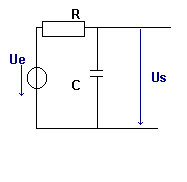
Ce filtre peut être constitué d'un circuit RL série
ou d'un circuit RC série.
Dans les 2 cas nous avons un diviseur de tension - même si elle ne sont pas en phase.
La répartition des tensions est fonction des valeurs ohmiques des éléments.
|
 |
Dans le cas RL
lorsque la fréquence augmente,
la réactance d'induction Xl augmente,
la tension Ul augmente alors que la tension Ur,
aussi tension de sortie Us diminue. |
Dans le cas RC
lorsque la fréquence augmente,
la réactance de capacité Xc diminue,
la tension Uc et donc la tension de sortie Us
diminue. |
La fréquence à laquelle on estime que le filtre fonctionne ( fréquence
de coupure fc ou quadrantale) est la fréquence qui produit une
atténuation de 3 dB par rapport au
signal d'entrée. Cette fréquence est celle où soit Xl =R
soit Xc = R.
fc = R / (2.p.L) ou fc = 1 / (2.p.R.C) [Hz]
A fc ,la tension de sortie est donc 0,707 fois plus petite que
celle d'entrée ( soit -3 dB)
ici, je détermine la fréquence de coupure pour un RL
:
|
ici, je détermine la fréquence de coupure pour un
RC :
|
|
|
|
|
Un filtre passe-haut atténue les courants de basses fréquences ("laisse
passer les hautes fréquences").
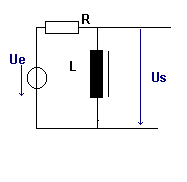 |
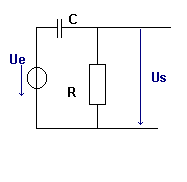
Ce filtre peut être constitué d'un circuit RL série
ou d'un circuit RC série.
Dans les 2 cas nous avons un diviseur de tension - même si elle ne sont pas en phase.
La répartition des tensions est fonction des valeurs ohmiques des éléments.
|
 |
Dans le cas RL
lorsque la fréquence augmente,
la réactance d'induction Xl augmente,
la tension Ul et donc la tension de sortie Us
augmente. |
Dans le cas RC
lorsque la fréquence augmente,
la réactance de capacité Xc diminue,
la tension Uc diminue alors que la tension Ur,
aussi tension de sortie Us augmente. |
La fréquence à laquelle on estime que le filtre fonctionne ( fréquence de coupure
fc ou quadrantale) est la fréquence qui produit une atténuation
de 3 dB par rapport au signal
d'entrée. Cette fréquence est celle où soit Xl = R
soit Xc = R.
fc = R
/ (2.p.L) ou fc
= 1 / (2.p.R.C) [Hz]
A fc ,la tension de sortie est donc 0,707 fois plus petite
que celle d'entrée ( soit -3 dB)
ici, je détermine la fréquence de coupure pour un RL
:
|
ici, je détermine la fréquence de coupure pour un
RC :
|
|
|
|