|
.

|
introduction
aux nombres complexes : leçon 1 |
introduction
Un nombre complexe est composé d'une partie réelle (axe x) et d'une partie imaginaire
(axe y)
Les nombres complexes sont très utilisés en électricité. Il permette
de définir une amplitude et un angle de déphasage en même temps.
La technique de calcul des nombres comlexes est très similaire à celle
des vecteurs.
Un nombre comlexe peut prendre 2 notations différentes :
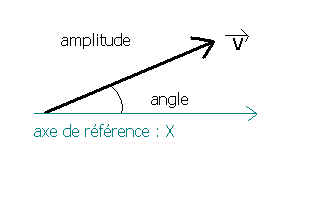
notation polaire
V = amplitude . e j angle
exemple : S = S e j
phi
|
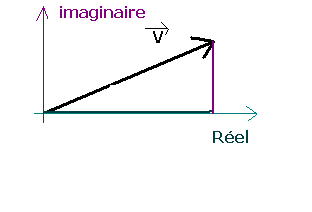
notation complexe
V = (Vx + jVy)
exemple . S = (P + jQ)
|
note : Il existe d'autres types de notations. Par exemple :
le j peut être remplacé par un i.
leçon 2 |
|
.
introduction
aux nombres complexes : leçon 2 |
le nombre imaginaire:
Dans les mathématiques traditionnelles, les nombres sont regroupés en
familles :
- les Entiers (positifs et négatifs : 3)
- les fractions ( 3/7)
- les irrationnelles ( p, 20,5 )
- etc..
Toutefois avec ces nombres, il est impossible de calculer une racine
carrée d'un nombre négatif (-20,5 , -1420,5).
On a donc imaginé un nombre qui se situe sur un autre axe que les nombres
réels.
L'unité de ce nombre est i (ou j)
et vaut (-1)0,5 ( racine carrée de -1).
(-16)0,5 étant égale à (-1*16)0,5 = -10,5
* 160,5 cela nous donne donc : 4 * i noté 4i ou 4j ou j4... Ce
nombre est purement imaginaire. Il est superposé à l'axe imaginaire.
Dans la pratique, il est plus courant qu'un nombre soit composé d'une
partie réelle et d'une partie imaginaire. Cela devient donc un nombre complexe. (
un nombre à deux dimensions selon illustration de la leçon1) .
Il est bon de savoir que
- 3i + 6i = 9i ( normal..)
- 4i * 5 = 20i (normal..)
- i * i = -1 ( le carré de la racine de -1 = -1)
- i3 = -i; ( -1 * i)
- i4 = 1 ( -1 * -1), on constate que le nombre obtenu tourne dans le plan
formé par l'axe des réels ( X) et des imaginaires (Y).
leçon 3
|
|
.
introduction
aux nombres complexes : leçon 3 |
passer d'une notation à l'autre
notation polaire -> rectangle
Vréel = | V| . cos angle
Vimaginaire= | V| . sin angle
exemple :P = |S| .cos phi , Q = |S| . sin phi
note : on parle aussi de S cis phi
|
notation rectangulaire-> polaire
|V| = ( Vr2 + Vi2)0,5
angle = arctangente Vi/Vr +k*p
[rad]
exemple :|S| = ( P2 + Q2)0,5
angle = arctangente Q/P +k*p
|
utilisation de la machine à calculer : P ->
R
Casio
entrez l'amplitude
P -> R
entrez l'angle
= (affiche Réel)
X->Y (affiche imaginaire) |
TI
entrez l'amplitude
X->Y
entrez l'angle
P->R (affiche Réel)
X->Y (affiche imaginaire) |
|
utilisation de la machine à calculer : R ->
P
Casio
entrez Réel
R -> P
entrez imaginaire
= (affiche amplitude)
X->Y (affiche angle) |
TI
entrez Réel
X->Y
entrez imaginaire
R->P (affiche amplitude)
X->Y (affiche angle) |
|
modifiez un ou plusieur valeur, l'autre notation sera mise à jour automatiquement
(cliquer une fois hors du champ text)
leçon 4 |
|
.
introduction
aux nombres complexes : leçon 4 |
|
|
|
.
introduction
aux nombres complexes : leçon 5 |
opérations de multiplication
Pour multiplier des nombres complexes, il faut faire le produit des
amplitudes et la somme des angles :
A = = |A| ejphi1;
B = |B| ejphi2; A
* B = |A|*|B| ejphi1 + phi2
exemples : I = 10 ej30
U = 230 ej0 ;
S = I * U
== 10*230 ej0+30= 2300 ej30
(donc S = 1991 + 1150i ,
soit P = 1991 [W] et Q = 1150 [var] )
seconde méthode :
A = a +
bi; B = c + di; A
* B = ( a +bi) * ( c+ di) = ac + adi + bci +bdi2
= ac-bd + i(ad + bc)
note : i2 = -1
I = 8,66 + 5i; U
= 230 + 0i; S = I *
U = (8,66 *230 - 5* 0) + ( 8,66*0 + 5 * 230)i = 1991 + 1150i
opérations de division :
Pour diviser deux nombres complexes, il faut faire le quotient amplitude
et la différence des angles
A = = |A| ejphi1;
B = |B| ejphi2; A
/ B = |A| / |B| ejphi1 - phi2
exemples : I = 10 ej60
U = 230 ej0 ;
Z = U / I
= 230 / 10 ej0-60= 23 ej-60
|
|
..
|