en savoir un peu plus ..

Math ++

Les logarithmes

estimation d'un log sans machine
extraire n'importe quelle racine de n'importe quel nombre - sans machine

calcul vetoriel

introduction
changement de notation
addition
soustraction
produit scalaire

nombres complexes

addition / soustraction
produit / quotient

thèmes associés

calcul de l'amplitude du champ tournant triphasé

Comment dit-on les grands nombres ?

et les très grands nombres ?

diaporama sur la résolution par le cercle unitaire

liens sur le web

introduction au calcul vectoriel : leçon 1

introduction :

Un vecteur est une flèche placée dans un espace à 2 (ou plus) dimensions

Le calcul vectoriel est utilisé par exemple pour la calcul de force, de courant ( électricité) ou autre.

Un vecteur est caractérisé par une longueur, un sens et une direction. Il peut aussi représenter un nombre à deux dimensions (l'une selon l'axe des réels et l'autre selon l'axe des imaginaires : on parle alors de notation complexe et de nombre complexe).

Il se note soit :

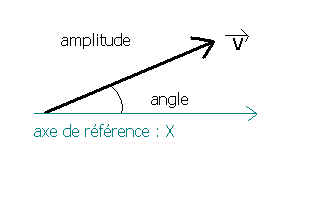
notation polaire

V = amplitude . e^{j angle}

exemple : S = S e^{j phi}

Vectphi.gif (2103 octets)

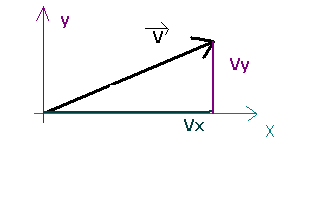
notation rectangulaire

V = (Vx; Vy)

exemple . S = (P; Q)

Vectrect.gif (2141 octets)

note : la notation d'un vecteur ce fait habituellement avec une flèche sur la lettre symbolisant le vecteur. Ici j'utilise un caractère gras souligné.

leçon 2

introduction au calcul vectoriel : leçon 2

passer d'une notation à l'autre

notation polaire -> rectangle

^{Vx = | V| . cos angle}

^{Vy = | V| . sin angle}

exemple :P = |S| .cos phi , Q = |S| . sin phi

notation rectangulaire-> polaire

|V| = ( Vx² + Vy²)^0,5

angle = arctangente Vy/Vx +k*p [rad]

exemple :|S| = ( P² + Q²)^0,5

angle = arctangente Q/P +k * p

utilisation de la machine à calculer : P -> R

Casio

entrez l'amplitude

P -> R

entrez l'angle

= (affiche X)

X->Y (affiche Y)

entrez l'amplitude

X->Y

entrez l'angle

P->R (affiche X)

X->Y (affiche Y)

utilisation de la machine à calculer : R -> P

Casio

entrez X

R -> P

entrez Y

= (affiche amplitude)

X->Y (affiche angle)

entrez X

X->Y

entrez Y

R->P (affiche amplitude)

X->Y (affiche angle)

leçon 3

introduction au calcul vectoriel : leçon 3

opérations d'addition :

Pour additionner des vecteurs, il faut additionner les valeurs selon X et les valeurs selon Y :

A = (a , b)	B = (c , d)	A + B =( a+c , b+d)
exemples :
I₁ = (3 , 5)	I₂= (9 , 2)	I₁ +: I₂ = (3+9 , 5+2) = (12 , 7)

calcul du courant dans le neutre: I_n= -(: I₁ + : I₂ + : I₃)

avec :

I₁ = (0 , 10) ;
I₂ = (8,66 , - 5)
I₃ = (-8.66, - 5) ( courant triphasé 10A en phase avec les tensions)

I_n= (8,66 - 8.66 , 10-5-5) = ( 0, 0)

leçon 4

introduction au calcul vectoriel : leçon 4

opérations de soustraction :

Pour soustraire deux vecteurs, il faut soustraire les valeur selon X et les valeurs selon Y :

A = (a , b)	B = (c , d) ;	A - B =( a-c , b-d)
exemples :
F1 = (3 , 5);	F2 = (9 , - 2) ;	F1 - F2 = (3-9 , 5+2) = (-6 , 7)

calcul d'une tension composée :

U_ph1 =(0, 230 )
U_ph2 = (200 , -115 )

U₁₂ = U_ph1 - U_ph2 =( -200 + 230 , 115) = (-20#50 , 345) [= 398 e^j120 ]

introduction au calcul vectoriel : leçon 5

Produit scalaire :

Pour faire le produit d'un nombre réel et d'un vecteur, on fait le produit des coordonées du vecteur par le réel.

A = (a , b)	e	e * A =( e* a , e*b) = (ae, be)
exemple :
Z = (3 , 5);	n =2	n * Z = (2 * 3 , 2 * 5) = (6 , 10)

On distingue 2 types de produit de vecteur : le produit vectoriel (dont je ne vous direz rien ) et le produit scalaire (dont je ne vous direz rien non plus)...